Пример решения задачи 10270
Условие По двум бесконечно длинным, прямым параллельным проводам текут одинаковые токи I = 60 А. Определить магнитную индукцию В в точке А, равноудаленной от проводов на расстояние d = 10 см. Угол β = π/3.
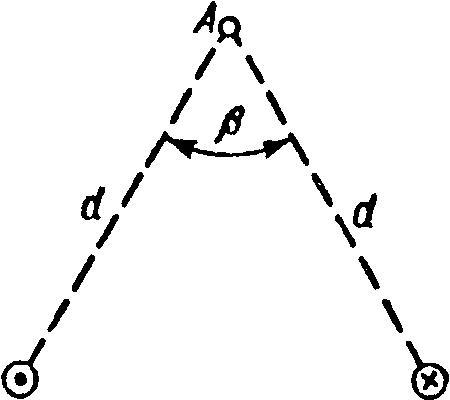
Краткое условие
I = 60 A
d = 10 см = 0,1 м
β = π/3
Найти
B ― ?
Решение
Запишем закон Био-Савара-Лапласа
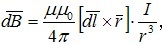
где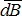 ― вектор магнитной индукции поля, создаваемого элементом проводника с током;
― вектор магнитной индукции поля, создаваемого элементом проводника с током;
μ ― магнитная проницаемость среды,
μ0 = 4π·10–7 Гн/м ― магнитная постоянная,
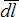 ― вектор, равный по модулю длине dl проводника и совпадающий по направлению с током;
― вектор, равный по модулю длине dl проводника и совпадающий по направлению с током;
I ― сила тока в проводнике,
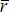 ― расстояние до проводника.
― расстояние до проводника.
Модуль вектора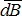 выражается формулой
выражается формулой
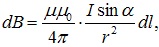
где I ― сила тока в проводнике;
r ― расстояние до элемента dl проводника.
α ― угол между векторами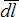 и
и 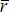
Выведем формулу напряженности магнитного поля, создаваемого бесконечно длинным прямым проводником с током на расстоянии a от него. Выделим элемент проводника длиной dx.
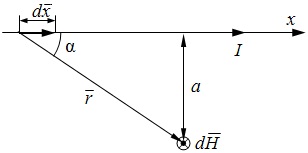
Он создает вектор напряженности Модуль вектора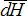 , значение которого
, значение которого
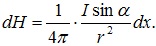
Из рисунка:
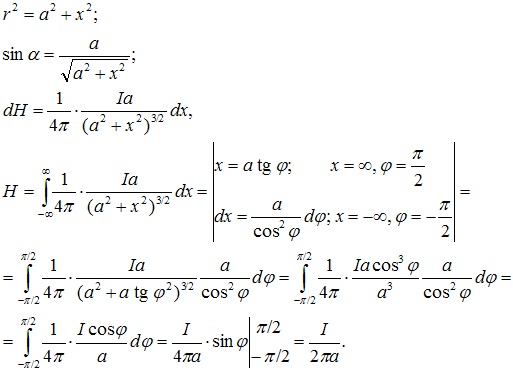
Учитывая, что индукция магнитного поля связана с напряженностью соотношением
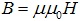
и a = d, для проводников задачи получим
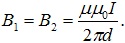
Изобразим векторное сложение векторов Модуль вектора 1 и Модуль вектора
1 и Модуль вектора 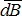 2.
2.
2α = 360°–90°–90°–β
2α = 180°–β
Суммарный вектор индукции магнитного поля определяется по принципу суперпозиции полей векторным сложением векторов
определяется по принципу суперпозиции полей векторным сложением векторов  1 и
1 и 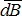 2:
2:
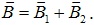
Так как в треугольнике со сторонами В1, В2 и В стороны В1 и В2 равны между собой, то это равнобедренный треугольник. Для этого треугольника:
γ = 180°–2α = 180°–(180°–β) = β.
Сторону В треугольника найдём по теореме косинуса:
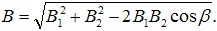
С учётом В1=В2 и cos60°=0,5 получим:
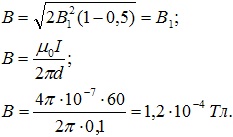
Ответ: В = 1,2·10–4 Тл.
Условие По двум бесконечно длинным, прямым параллельным проводам текут одинаковые токи I = 60 А. Определить магнитную индукцию В в точке А, равноудаленной от проводов на расстояние d = 10 см. Угол β = π/3.

Краткое условие
I = 60 A
d = 10 см = 0,1 м
β = π/3
Найти
B ― ?
Решение
Запишем закон Био-Савара-Лапласа
где
μ ― магнитная проницаемость среды,
μ0 = 4π·10–7 Гн/м ― магнитная постоянная,
I ― сила тока в проводнике,
Модуль вектора
где I ― сила тока в проводнике;
r ― расстояние до элемента dl проводника.
α ― угол между векторами
Выведем формулу напряженности магнитного поля, создаваемого бесконечно длинным прямым проводником с током на расстоянии a от него. Выделим элемент проводника длиной dx.

Он создает вектор напряженности Модуль вектора
Из рисунка:
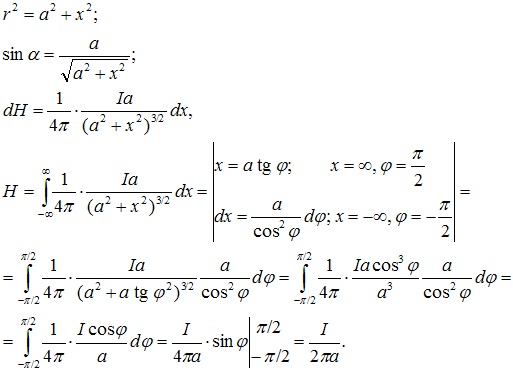
Учитывая, что индукция магнитного поля связана с напряженностью соотношением
и a = d, для проводников задачи получим
Изобразим векторное сложение векторов Модуль вектора

2α = 360°–90°–90°–β
2α = 180°–β
Суммарный вектор индукции магнитного поля
Так как в треугольнике со сторонами В1, В2 и В стороны В1 и В2 равны между собой, то это равнобедренный треугольник. Для этого треугольника:
γ = 180°–2α = 180°–(180°–β) = β.
Сторону В треугольника найдём по теореме косинуса:
С учётом В1=В2 и cos60°=0,5 получим:
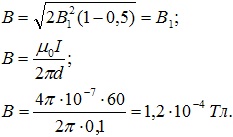
Ответ: В = 1,2·10–4 Тл.